Emulsion Stability and Testing
Emulsions encompass a vast number of everyday materials and products, including foodstuffs, personal care items, and pharmaceuticals. Topical emulsions of both the oil-in-water (o/w) and water-in-oil (w/o) types are commonly used to improve properties such as aesthetics and ease of application, among others. Emulsions may also be used to deliver multiple active pharmaceutical ingredients (APIs) of differing solubility, present an API in a format that improves the distribution and/or permeation on application, or improve patient compliance for aesthetic reasons. However, as emulsions are inherently thermodynamically unstable, understanding the theoretical factors influencing emulsion stability is critical to the emulsion formulator.
Emulsion Stability
The process by which an emulsion coalesces (completely breaks i.e., the system separates into bulk oil and water phases), is generally considered to be governed by four different droplet loss mechanisms: Brownian flocculation, creaming, sedimentation flocculation, and disproportionation, shown schematically in Figure 1. The first three are the primary methods by which emulsions are destabilized, though all four processes may occur simultaneously and in any order1, 2.
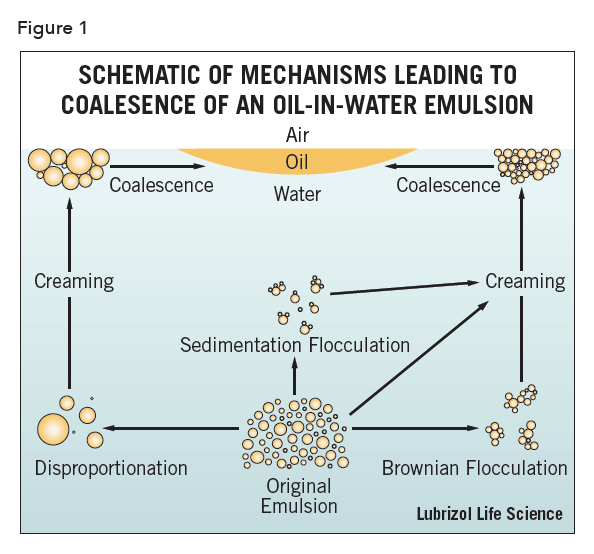 The processes of creaming, flocculation, and coalescence are well demonstrated by taking an emulsion of limited stability and centrifuging it at low speeds or various lengths of time. For oils with a density less than water (which will be assumed unless otherwise noted), an initial “rising” of the cream is observed. Then, as larger droplets rise and concentrate, they begin to appear at the top. Finally, the drops coalesce to form a separate layer of oil on top.
The processes of creaming, flocculation, and coalescence are well demonstrated by taking an emulsion of limited stability and centrifuging it at low speeds or various lengths of time. For oils with a density less than water (which will be assumed unless otherwise noted), an initial “rising” of the cream is observed. Then, as larger droplets rise and concentrate, they begin to appear at the top. Finally, the drops coalesce to form a separate layer of oil on top.
Creaming derives its name from the most commonly known example of a de-emulsification process – the separation of milk into its separate cream (curd) and skim milk (whey) components. Creaming is not an actual breaking but a separation of the emulsion into two emulsions, one of which (the cream) is richer in the disperse phase than the other. Creaming is the principal process by which the disperse phase separates from an emulsion and is typically the precursor to actual coalescence.
The creaming rate (or settling rate for disperse phases that are more dense than the continuous phase) can be estimated from the Stokes’ equation:
ʋ = 2𝑟𝑟% 𝜌𝜌 − 𝜌𝜌( 𝑔𝑔/9𝜂𝜂
where, ʋ is the creaming (settling) rate, r is the droplet radius, ρ is the density of the droplet, ρo is the density of the dispersion medium, η is the viscosity of the dispersion medium (continuous phase), and g is the local acceleration due to gravity.
The density difference, , (ρ-ρo) is negative for creaming (an o/w emulsion) but positive for settling (a w/o emulsion). The Stokes equation shows that creaming is inhibited by a small droplet radius, a highly viscous continuous phase, and a low density difference between the oil and water phases. Substituting “typical” values into the equation, i.e., r ~ 1 μ, Δρ ~ 0.2 g·cm-3, and η ~ 1 mPa·s gives a creaming rate of ~ 5 cm per day, which is substantial. A creaming rate of < 1 mm per day is considered negligible.
Flocculation can be generally defined as the aggregation of droplets to give 3-D clusters without coalescence occurring. Importantly, all droplets maintain their own integrity and remain as totally separate entities. It results when there is a weak net attraction between droplets and arises through various mechanisms, the discussion of which is beyond the scope of this Technical Brief3-5.
Flocculation may be subdivided for convenience into two general categories: that resulting from sedimentation aggregation and that from Brownian motion aggregation of the droplets. In polydisperse (“real”) emulsions, droplets of different sizes cream at different rates, which leads to a tendency for the faster-moving (larger) droplets to collide with, and potentially trap, slower moving (smaller) droplets. In sedimentation aggregation it is assumed that all the paths in sedimentation are vertically linear; Brownian aggregation is the result of random Brownian movement of the droplets. In both cases a frequency factor for sedimentation encounters can be defined4. Both processes occur simultaneously in a typical emulsion and therefore cannot be rigorously separated. Nevertheless, an estimate of the relative rates of each type of flocculation can be made from6:
Γmax = 2π g r4 / 3kbT
where kb is the Boltzmann constant and T is absolute temperature in Kelvin.
When Γmax>10, Brownian aggregation is negligible; when max 0.1 sedimentation aggregation is negligible.
Because the magnitude of the forces involved is different for the two flocculation processes, the structure of the 3-D droplet clusters is different.
Finally, flocculation may also be divided into fast flocculation and slow flocculation7. The former occurs when the smaller droplets disappear more rapidly than the larger ones as a result of the different rates of movement under gravity or in forced convection, leading to an increased collision rate (orthokinetic aggregation). The latter occurs when the build-up of large metastable structures slows first as a result of the energy barrier between droplets and then the formation of droplet-free spaces between aggregates and the heavier aqueous phase o/w emulsions; the consequence is called hindered creaming.
Disproportionation is a process – often referred to as Ostwald ripening – dependent on the diffusion of disperse phase molecules from smaller to larger droplets through the continuous phase. The pressure of dispersed material is greater for smaller droplets than larger droplets as shown by the Laplace equation:
P = 2γ/r
where P is the Laplace pressure, γ is the surface tension, and r is the droplet radius.
This pressure differential between small and large droplets constitutes the driving force for diffusion, but the rate of diffusion depends on the solubility of the dispersed phase in the continuous phase. The higher the disperse phase volume, the greater its relative vapor pressure (and thus the solubility) will be, as given by the kelvin equation:
ln [Po / P] = 2γ Vm /rRT
where P is the vapor pressure of the liquid droplet, Po is the vapor pressure of the bulk liquid, γ is the surface tension, r is the droplet radius, and V is the molar volume of the disperse phase.
The diffusion rate is also impacted directly by the viscosity of the continuous phase as described by the Stokes-Einstein equation:
D = kbT/ 6πηr
where D is the diffusion coefficient of a droplet and is the continuous phase viscosity.
The measurement of both the droplet size and size distribution of emulsions is a critical metric. A variety of sizing techniques are available but, from Figure 1, it is obvious that image analysis (for regular emulsions) should be a prime candidate.
Emulsion Stability Testing
Stability testing is an integral part of emulsion development work. A discussion of drug stability testing methods and kinetics is beyond the scope of this Technical Brief and the reader is referred to other books and review papers on the subject8-10.
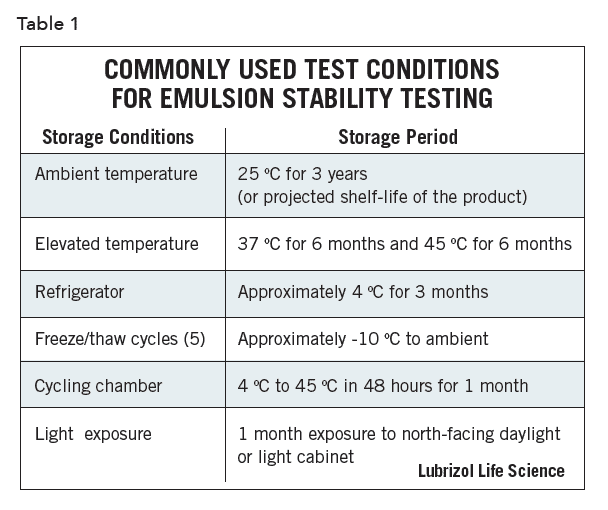
The emulsion formulator is generally concerned with understanding the effects of storage and shipping conditions on shelf-life, which may include extremes of temperatures, exposure to sunlight, vibration, and humidity. Hence, formulations are stored under standardized test conditions and carefully examined at periodic intervals. Table 1 lists general conditions commonly and historically used to evaluate emulsion stability, though regulated emulsion products must be tested in compliance with applicable ICH guidelines. Further, although freeze-thaw has been widely used as an accelerated path to judge emulsion stability, it is not appropriate to rely solely on it. The cycling of temperature in freeze-thaw experiments affects parameters other than those directly related to creaming, which is the actual mechanism of emulsion instability.
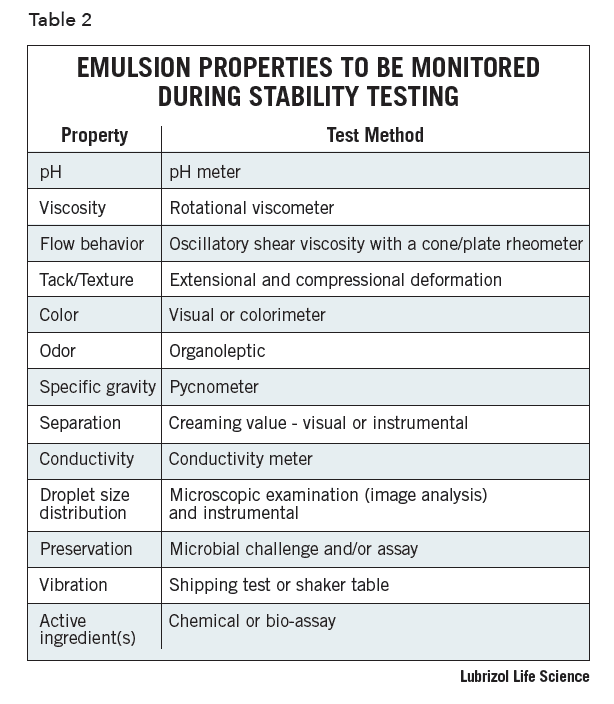
 Laboratory batches are generally stored in glass jars to evaluate the inherent stability of the emulsion. The use of glass jars permits easy observation and physical measurements at regular intervals. However, ultimately the emulsion must also be evaluated in the intended final packaging, as this may impact the stability due to interfacial wetting behavior, permeation, or leaching of components into or out of the packaging material. Table 2 lists properties that are important to full understand, including the characteristics and stability of an emulsion formulation. The number of properties is quite extensive, and all the instrumentation required may not be available to many formulators. Ideally, all these tests should be conducted on a final formulation but it is not practical, nor necessary, to conduct the total battery of tests on all preliminary formulations. Typically, initial formulations are screened for changes in pH, viscosity, flow behavior, odor, and physical separation at elevated temperatures.
Laboratory batches are generally stored in glass jars to evaluate the inherent stability of the emulsion. The use of glass jars permits easy observation and physical measurements at regular intervals. However, ultimately the emulsion must also be evaluated in the intended final packaging, as this may impact the stability due to interfacial wetting behavior, permeation, or leaching of components into or out of the packaging material. Table 2 lists properties that are important to full understand, including the characteristics and stability of an emulsion formulation. The number of properties is quite extensive, and all the instrumentation required may not be available to many formulators. Ideally, all these tests should be conducted on a final formulation but it is not practical, nor necessary, to conduct the total battery of tests on all preliminary formulations. Typically, initial formulations are screened for changes in pH, viscosity, flow behavior, odor, and physical separation at elevated temperatures.
 Emulsions have a long history of use and are widely used in many products encountered in everyday life. Understanding the theoretical considerations in emulsion formulation and having the ability and proper instrumentation to fully characterize and monitor stability of an emulsion system is highly beneficial in providing a superior product in a time efficient manner.
Emulsions have a long history of use and are widely used in many products encountered in everyday life. Understanding the theoretical considerations in emulsion formulation and having the ability and proper instrumentation to fully characterize and monitor stability of an emulsion system is highly beneficial in providing a superior product in a time efficient manner.
References
- Becher, Emulsions: Theory and Practice, Reinhold Publishing Corp., New York (1957)
- Becher (Ed), Encyclopedia of Emulsion Technology, Volume 1: Basic Theory, Marcel Dekker, New York (1983)
- Cowell and B. Vincent, J. Colloid and Interface Science, 87 518 (1982)
- Dickinson and G. Stainsby, Colloids in Food, Applied Science Publishers, London (1982)
- D. Goddard and B. Vincent (eds), Polymer Adsorption and Dispersion Stability, ACS Symposium Series 240, America Chemical Society, Washington DC (1984)
- R. Reddy and H. S. Olger, J. Colloid and Interface Science, 79 105 (1981)
- A. J. S. van Boekel and P. Walstra, Colloids and Surfaces, 3 99 (1981)
- A. Connors, G. L. Amidon and J. S. Valentino, Chemical Stability of Pharmaceuticals: A Hand- book for Pharmacists, John Wiley, New York (1986)
- Grimm and K. Krummen (eds), Stability Testing in the EC, Japan and the USA: Scientific and Regulatory Requirements, Wissenschaftliche Verlagsgesellschaft, Stuttgart (1993)
- Wells, Pharmaceutical Pre-formulation: The Physicochemical Properties of Drug Substances, Ellis Horwood, Chichester (1988)
